 |
In this clip the class is discussing the penny on the checkerboard problem (click for more details).
The students initially want to raise 2 to the 64th power, but then they decide it should be 63rd by looking at the first few squares. A student asks about using a linear function to model the situation and the teacher gives a counterexample as to why linear would not work. This is one opportunity to start pointing out the difference between exponential relationships and linear relationships.
|
 |
While discussing the penny on the checkerboard problem the teacher asks the class what it means to double something (click for more details).
This creates a discussion about how multiplying by 2 is equivalent to doubling. The teacher questions the student until he is specific about what is actually being multiplied by 2 in order for something to double. The teacher recaps the idea for the other students. This allows her to segue into a discussiong of what it means to double every 5 squares.
|
 |
The teacher asks the students about creating a formula for bacteria doubling every 10 minutes (click for more details).
She asks for a formula, despite the fact that the students have NOT had the formal definition of an exponential function yet. This approach will help give meaning to each part of the exponential formula. She relates this situation to function composition and then changes the situation so the number of bacteria increase by 60% so the students must think about how the formula would change.
|
 |
In this clip the teacher is going over the rules of exponents with the students (click for more details).
She has the students state WHY the rules work, not just what they are. In order to understand exponential functions they need to have these understandings. She is also reinforcing the terminology of base as the number that is being repeatedly multiplied. She also gives meaning behind why they are exploring properties of exponents.
|
 |
In this clip the teacher leads a discussion about raising a number to a rational exponent (click for more detials).
They discuss what it means to raise something to the 1/2 power. This is their first encounter in this class with non-integer exponents.
|
 |
In this clip the teacher leads a discussion abou what makes a situation exponential (click for more details).
This is the 2nd day of the exponential module and the teacher is taking the opportunity to push the students to speak about exponential functions in a meaningful way. They discuss several of the characteristics of exponential functions.
|
 |
The teacher is discussing the pennies on a checkerboard problem and asks how to talk about parts of a penny (click for more details).
She makes the assumption that they can use and discuss parts of a penny. They are dealing iwth the situation where the pennies double every 5 squares and she asks how many will be on the last square. Thus the students are left with developing the forumlua for doubling time.
|
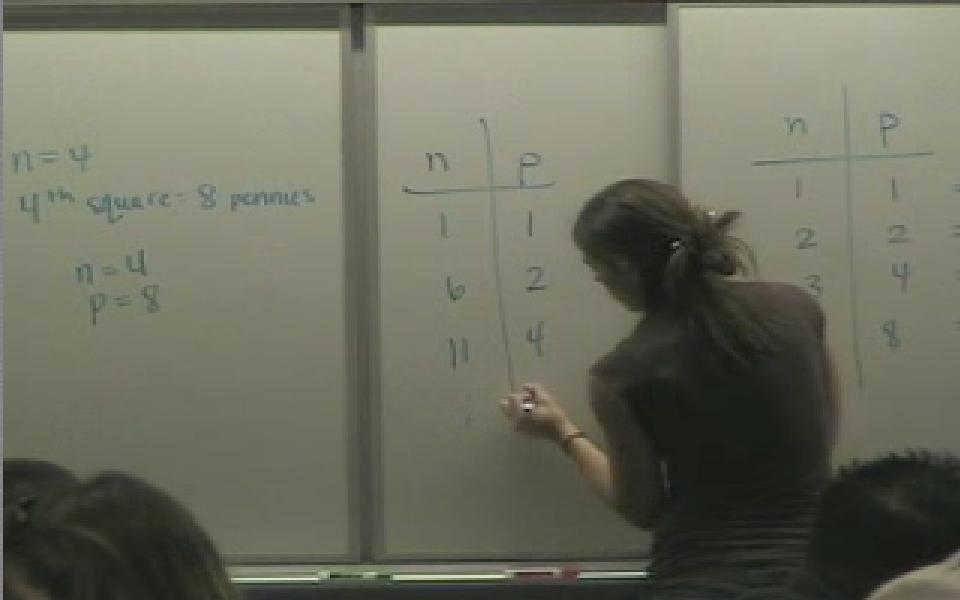 |
In this clip the teacher has the students share their solutions to the problem from the previous clip (click for more details).
This clip is a conintuation from the previous clip an dthe teacher has the students share and judge each others solutions. She is able to focus them on key elements as this happens and gives them strategies for checking their answers.
|
 |
In this clip the teacher is discussing the formula from the previous clip with a group that is having trouble understanding the formula (click for more details).
It is important to realize that many students will struggle with the creation of this formula. This is an exmaple of how a teacher can deal with these difficulties.
|
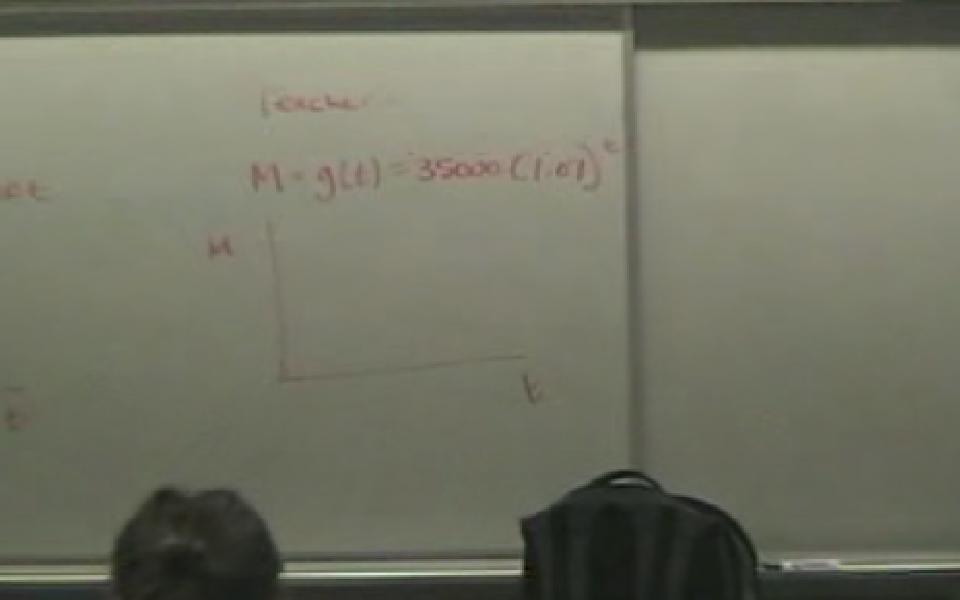 |
In this clip the instructor discusses the where the multiplicative factor comes from in an exponential function and how it works as the input is increased by 1 year (click for more details).
She demonstrates the multiplicative relationship and why it has an exponential relationship. As she is writing on the board she is reinforcing the term factor. She uses the slide to exhibit the difference between the constant rate of change and the constant percent change and she creates a discussion about why the amount of increase is going up.
|
 |
In this clip the teacher is looking at the teacher’s salary problem and the growth factor of 1.07 (click for more details).
She asks them what about for 3 years and what by percentage does the salary increase. 21% is a common answer from the students after some group discussion. This creates an opportunity for her to examine the affect of the growth factor and how to use it to solve this type of problem.
|
 |
When the group gives their solution to the above problem, the teacher writes their suggestion on the board to create a discussion (click for more details).
This is a follow up to the above clip and demonstrates how the teacher uses a student solution to create a discussion by having the other students judge its validity. During the discussion the teacher is constantly reinforcing the terminology of the classroom.
|
 |
In this clip the teacher leads a discussion with the students about why different ways of compounding would make sense (click for more details).
This is one way of introducing the bank account formulas for compound interest. She is getting them involved and helping them get an intuitive sense as to why the compound interest formulas make sense. They are also gaining a sense of the value of increased compounding periods.
|
 |
After the above discussion, the teacher goes back to a problem they were working on concerning a bank account with 1000 at 8% compounded monthly (click for more details).
The teacher is using this opportunity to discuss the monthly growth factor and develop the compound interest formula. This will help the students make sense of the formula and why they divide the interest rate by the number of compounding periods. She also asks about the growth rate and has them identify what they would make each month. She then extends the period to 7 years. Then they create the general formula and discuss the components as a class.
|
 |
In this clip they discuss the annual growth factor (click for more details).
They have just finished talking about the monthly growth factor and developing the general formula for compound interest, now the teacher asks them how to find the annual growth factor. The students initially want to multiply the monthly growth factor by 12. The teacher gives them a hint by reminding them what they did previously, but the students are still struggling.
|
 |
The teacher is going over the formula for a bank account with a principal amount of 1000 and a rate of 8% compounded monthly (click for more details).
As a class they go through each part of the formula, discussing why they make sense. The teacher makes sure the students are using the appropriate terminology during the discussion.
|
 |
This is a way to introduce students to compounding continuously (click for more details).
They each get an account and observe what happens as they compound more and more times. The instructor uses a slide to show them how it levels off.
|
 |
In this clip the students are finding what exponent completes the given equations (click for more details).
The teacher is also bringing in logarithms. She is allowing them to estimate which keeps the students from using the calculator and turning logarithms into a procedural routine, as can normally be the case. It is not until the end of this exercise that she gives logarithmic notation.
|
 |
In this clip the teacher is discussing a property of logarithms (click for more details).
This is an example of how the product to sum formula for logarithms can be derived by building on the students’ understanding of the output of logs being exponents.
|
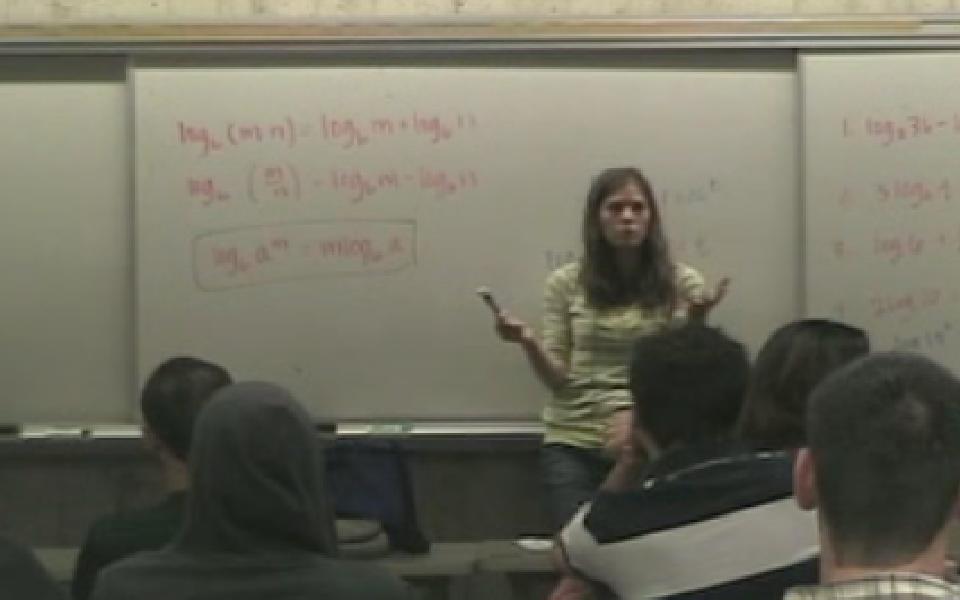 |
In this clip the students are solving an equation in which the exponent is unknown (click for more details).
The teacher requires justification at this point. It is important that students understand why this works. It can often be necessary for the teacher to push students to create appropriate justifications for their conjectures.
|

