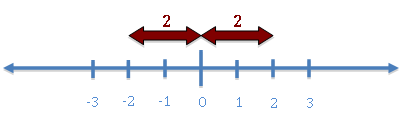
The “absolute value” of a number is simply the distance the number is from zero. When we take the absolute value, we just want to know the “value” of its distance from zero.
What is the absolute value of 2? What is the absolute value of -2?
Both 2 and -2 are the same distance from zero – they are both 2 units from zero. So, the “absolute value” of 2 is 2. The “absolute value” of -2 is also 2:

The notation for absolute value is two straight lines on each side of a number. So, the absolute value of the number x would be written:
$$
\left| x \right|
$$
So, we can write “the absolute value of -2 is 2” as:
$$
\left| { - 2} \right| = 2
$$
You can think of absolute value as simply making the number inside the absolute value sign positive. Keep in mind that the reason you do this is because the number’s distance from zero is always going to be positive.
Determine the value of the following:
1. $$
\left| { - 51.5} \right|
$$
Solution: Just find the distance of the value inside the absolute value sign from zero. It is 51.5 units from zero, so:
$$
\left| { - 51.5} \right| = 51.5
$$
2. $$
\left| {67} \right|
$$
Solution: Just find the distance of the value to zero. It is 67 units from zero, so: $$
\left| {67} \right| = 67
$$
3. $$
\left| { - 8 + 5} \right|
$$
Solution: At first, treat the absolute value like a set of parentheses. Simplify the inside of the absolute value and then take the absolute value of that number (make it positive if it is not):
$$
\left| { - 8 + 5} \right| = \left| { - 3} \right| = 3
$$
4. $$
\left| y \right|
$$
, where y is a real number.
Solution: BE CAREFUL! You might be tempted to say that the absolute value of y is just y. Unfortunately, it’s not that simple:
Suppose y = 3. Then, this idea will work just fine: You will have $$\left| 3 \right| = 3$$ , which is true.
However, what if y = -3? Then, if we claim that $$ \left| y \right| = y $$ , and we plug in -3 for y, we get: $$ \left| { - 3} \right| = - 3 $$ . This is NOT true.
So, for this problem, $$ \left| y \right| = y $$ only when y is positive. When y is negative, $$ \left| y \right| = - y $$ (because that negative sign will go away when we plug in y, since y is negative). In mathematics, we write a solution like this using the following notation:
$$
\left| y \right| = \left\{ \matrix{
y\;\;\;\;\;\;\;when\;y \ge 0 \cr
- y\;\;\;\;\;when\;y < 0 \cr} \right.
$$
Now, we’re ready to solve some equations involving absolute value:
Solve for x. That is, find the values of x that make the equation true:
$$
\left| x \right| = 7
$$
Remember that when we “solve for x”, we are simply looking for all values of x that make the equation true.
So, in this case, we need to find a number or numbers that give 7 when we take the absolute value.
Inside the absolute value sign, we can have either a positive or a negative 7 to give a value of 7. So, in this case, $$ x = 7 $$ or $$ x = - 7 $$ .
Solve for y. That is, find the values of y that make the equation true:
$$
\left| y \right| = - 9
$$
Solution: There are no solutions to this problem. The absolute value can never be negative. Remember that it can be thought of as the distance from zero, and we cannot have a negative distance.
Let’s explore a slightly more difficult equation:
Solve for z. That is, find the values of z that make the equation true:
$$
\left| {3z - 7} \right| = 12
$$
Now, again we have an absolute value. We know that when we take the absolute value, we get 12. So, the stuff inside the absolute value sign must either equal 12 or -12. Either of these, when we take the absolute value, will give us 12 as our final answer. So, to solve an equation like this, we really need to solve two equations: $$ 3z - 7 = 12 $$ and $$ 3z - 7 = - 12 $$
So, we need to solve linear equations here, and we get:
Solution 1:
$$
3z - 7 = 12
$$ (add 7 to each side):
$$
3z = 19
$$ (divide by 3 on each side):
$$
z = {\large{{19} \over 3}}
$$
Solution 2:
$$
3z - 7 = - 12
$$ (add 7 to each side):
$$
3z = - 5
$$ (divide by 3 on each side):
$$
z = {\large{{ - 5} \over 3}}
$$
So, in this equation, z can equal $$ {\large{{19} \over 3}} $$ or $$ - {\large{5 \over 3}} $$
Solve for n. That is, find the values of n that make the equation true:
$$
\left| {n + 3} \right| = \left| {4n} \right|
$$
This equation is somewhat more complicated. We know that the absolute values must be equal, but this time, there are absolute values on both sides.
One solution is fairly obvious. When $$ n + 3 = 4n $$ , their absolute values must also be equal (since each side will be the same number). So, we can solve this linear equation first:
$$
n + 3 = 4n
$$ and so,
$$
3 = 3n
$$ and finally,
$$
n = 1
$$
It is always good to check your answer when you solve an equation, and it is especially important in absolute value problems. There are times when solutions in these problems will not work (See Example 7). So, let’s check our answer of $$n = 1$$.
$$
\eqalign{
& \left| {n + 3} \right| = \left| {4n} \right| \cr
& \left| {1 + 3} \right| = \left| {4\left( 1 \right)} \right| \cr
& \left| 4 \right| = \left| 4 \right| \cr
& 4 = 4 \cr}
$$
So, this solution works.
We are not done, yet, though. The insides of the absolute value could also be negative and still be equal. If both of the insides of the absolute values are negative, we get:
$$
- \left( {n + 3} \right) = - \left( {4n} \right)
$$
However, we can just divide both sides by -1 and get back to the equation we just solved above:
$$
n + 3 = 4n
$$
So, this will once again get us the solution $$n = 1$$ .
So, what if the inside of one of the absolute values was negative and the other was positive? This, too, would work. For instance: $$
\left| { - 3} \right| = \left| 3 \right|
$$
. So, to get another solution, we can also multiply one of the sides by -1 and solve this equation:
$$
- \left( {n + 3} \right) = 4n
$$
[Note: Does it matter which side we make negative? No. If we wanted, we could multiply both sides by -1 at any time and switch the side that is negative. It would still be the same equation.]
So, to solve this, first we must use the distributive property to distribute the negative and get:
$$
- n - 3 = 4n
$$
Now, solving this linear equation, we get:
$$ - n - 3 = 4n$$ and so,$$ - 3 = 5n$$ and finally,$${\large{{ - 3} \over 5}} = n$$.
So, let’s check this answer, too:
$$
\eqalign{
& \left| {n + 3} \right| = \left| {4n} \right| \cr
& \left| { - {3 \over 5} + 3} \right| = \left| {4\left( { - {3 \over 5}} \right)} \right| \cr
& \left| {{{12} \over 5}} \right| = \left| { - {{12} \over 5}} \right| \cr
& {{12} \over 5} = {{12} \over 5} \cr}
$$
And so, this solution also works. So, our two solutions are 1 and $$
{\large{{12} \over 5}}
$$
.
Solve for x. That is, find the values of x that make the equation true:
$$
\left| {x - 2} \right| = 3x + 1
$$
Just as the previous two examples, this problem could potentially have more than one solution, since the inside of the absolute value can either be positive or negative. So, either $$
x - 2 = 3x + 1
$$ or $$ - \left( {x - 2} \right) = 3x + 1
$$ or both. Let’s solve the first for x.
$$
x - 2 = 3x + 1
$$
$$
- 2 = 2x + 1
$$
$$
- 3 = 2x
$$
And so:
$$
x = - {\large{3 \over 2}}
$$
So, let’s try this in the equation:
$$
\left| {\left( { - {\large{3 \over 2}}} \right) - 2} \right| = 3\left( { - {\large{3 \over 2}}} \right) + 1
$$
$$
\left| {\left( { - {\large{7 \over 2}}} \right)} \right| = \left( { - {\large{9 \over 2}}} \right) + 1
$$
But then,
$$
\left| {\left( { - {\large{7 \over 2}}} \right)} \right| \ne - {\large{7 \over 2}}
$$
Since:
$$
\left| {\left( { - {\large{7 \over 2}}} \right)} \right| = {\large{7 \over 2}}
$$
So, this first possible solution does not work.
Now, let’s solve the second linear equation:
$$
- \left( {x - 2} \right) = 3x + 1
$$
$$
- x + 2 = 3x + 1
$$
$$
1 = 4x
$$
And so:
$$
x = {\large{1 \over 4}}
$$
Now we just need to check this second possible answer:
$$
\left| {\left( {{\large{1 \over 4}}} \right) - 2} \right| = 3\left( {{\large{1 \over 4}}} \right) + 1
$$
$$
\left| {\left( { - {\large{7 \over 4}}} \right)} \right| = \left( {{\large{3 \over 4}}} \right) + 1 = {\large{7 \over 4}}
$$
And this is true. So, this solution works.
Thus, our only solution for this problem is: $$
x = {\large{1 \over 4}}
$$
Some practice problems to check your skills:
1. $$
\left| {3x - 2} \right| = 4
$$
Think about it for a moment and then access this link ![]() to view answer.
to view answer.
2. $$
\left| {7y + 8} \right| = - 5
$$
Think about it for a moment and then access this link ![]() to view answer.
to view answer.
3. $$
\left| {2x - 2} \right| = x + 3
$$
Think about it for a moment and then access this link ![]() to view answer.
to view answer.
4. $$
\left| {x - 5} \right| = 5x
$$
Think about it for a moment and then access this link ![]() to view answer.
to view answer.
5. $$
\left| {4x - 6} \right| = \left| {2x} \right|
$$
Think about it for a moment and then access this link to ![]() view answer.
view answer.