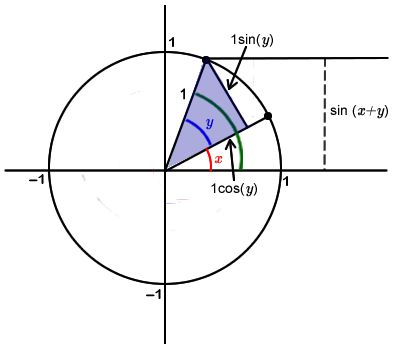Consider how we might estimate our walking distance to the Washington Monument given that we know the Monument height is 555 feet and the approximate angle of our line of sight to the top of the monument is 25 degrees. Can you identify a function that we’ve previously studied that would be useful for relating the measure of an angle to a length?
In Module 7, we investigated angle measure and trigonometric functions in the context of the unit circle. We then defined the sine and cosine functions and used these functions to model periodic behavior. We will leverage this knowledge of angle measure and trigonometric functions to explore the special relationships that exist between angles and lengths, where the lengths are sides of a right triangle.
Triangle trigonometry was known by Greek mathematicians as early as the 4th century BC and was used to find measurements that could not be directly determined. Today, many professions such as engineers, carpenters and surveyors continue to use knowledge of triangle relationships and triangle trigonometry for this same purpose. A surveyor uses triangle trigonometry to assist road builders in determining the grade of a new road. An architect uses triangle trigonometry to determine the depth of an overhang needed to shade a window, based on the angle of the winter sun. The early Greeks also developed a form of spherical trigonometry that allowed them to determine the exact times of the rising and setting of the zodiacal signs.
Prior to beginning this module, reflect on how we defined the sine function in the context of a unit circle. Can you determine how to use the sine function to relate the measure of angle and a side of a right triangle? We begin the module by exploring this question and will return to the Washington Monument question later (section 4) in the module.
Contents
1. Triangle Trigonometry and Sine
2. Triangle Trigonometry and Cosine
3. The Tangent Functions
4. Tangent and the Unit Circle
5. Trigonometric Identities
Overview of Module: In this module we first develop the meaning of sine, cosine and tangent functions in a right triangle context. We then practice using these ideas in applied problems that involve quantities that can be related with right triangle relationships. We conclude the chapter by deriving various trigonometric identities that relate the trigonometric functions to one another. These identities will be useful for solving problems involving trigonometric functions in your future mathematics and science courses.
1. Triangle Trigonometry and Sine
Recall that an angle measure q represents an amount of opening of the two rays of an angle. We learned that this amount of opening can be measured by constructing a circle centered at the vertex of the angle and determining the proportion of a circle’s circumference subtended (or cut off) by the angle’s rays. We expressed this proportion as a fraction or as a percent of the circle’s circumference that is subtended by the angle’s rays.
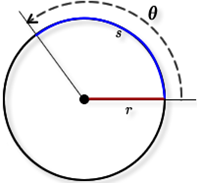
Figure 8-1
If our goal is to express the angle measure in radians we can multiply the percentage of the circle subtended by the angle’s rays by 2π, since the circumference of every circle is 2π radii. Similarly, if we want to express the angle measure in degrees, we can multiply the percentage of the circle cut off by the angle’s rays by 360 degrees since there are 360 degrees in a full circle.
We also learned in Chapter 7 that the sine and cosine functions accept an angle measure as input and produce a length measured in radii or lengths of a circle’s radius as output.
We can use these relationships to develop the meaning of the trigonometric functions in a right triangle trigonometry context. Keep these relationships in mind as we investigate how the sine function relates an angle measure and the sides of a right triangle. Recall that a right triangle is one in which one angle has a measure of 90 degrees or $${\large\frac{π}{2}}$$ radians. The side opposite the 90-degree angle is called the hypotenuse. The other two sides of a right triangle are commonly called the legs of the right triangle.
Example 1. The Eiffel Tower and Determining Angles Using Sine
As a tourist approaches the 1063-foot tall Eiffel Tower he stops to peer at the top of the tower with his range finder. The range finder reveals that the top of the tower is 1500 feet away from his position on the ground (Figure 8-2).
- Determine the measure of the angle formed by the beam-line that the ranger makes with the top of the tower and the line of sight (labeled d in Figure 8-2) of the tourist to the base of the tower.

Figure 8-2
Notice that we can represent the problem situation as a right triangle, where the line representing the height of the tower is one leg of a right triangle, the distance d of the tourist from the base of the tower is the other leg, and the beam-line from the ranger to the top of the tower is the hypotenuse.
Since our goal is to determine the value of q, we can use our knowledge of unit circle trigonometry to find the measure of the angle. Recall that the measure of an angle is the proportion of a circle’s circumference that the rays of the angle cut off.
By using the hypotenuse of 1500 feet as the radius of a circle, we can construct a circle centered at the tourist’s location (Figure 8-3). We also recall that the sine of an angle of measure q inscribed in a unit circle is defined to be the y-value of the ordered pair on the unit circle measured in radii.
To determine the height of the Eifel tower in radii we divide its height in feet by 1500 feet (or 1 radius-length).

Figure 8-3
Solution
We write $$\sin (\theta ) = {\large\frac{{1063}}{{1500}}} \approx 0.7087$$ radians.
Since our goal is to determine the value of $$\pi$$, we use the inverse sine function (also called arcsine) to determine the angle measure that corresponds to $$\frac{{1063}}{{1500}}$$ radians.
\[\arcsin (\sin (\theta )) = \arcsin \left( {\frac{{1063}}
{{1500}}} \right)\]
Recall that the arcsine is defined as the inverse of the sine function on a restricted domain of $$[-\pi/2,\;\pi/2]$$, and we are interested in a value of θ in this interval. Since composing a function with its inverse returns the original input value, we have that
\[\theta = \arcsin \left( {\frac{{1063}}{{1500}}} \right) \approx 0.7876\; \mathrm{radians,\;or}\; 45.13\; \mathrm{degrees.}\]
Example 2. Determining Angles Using Sine
Using the same approach, determine the measure of the angle formed by the beam-line of the ranger and the direct distance d of the tourist from the base of the tower, given that the ranger is 1100 feet from the top of the tower, as shown in Figure 8-4.

Figure 8-4
Think about it for a moment and then access this link  to view our answer.
to view our answer.
The 1110-foot hypotenuse becomes the constructed circle (Figure 8-4). Since 1 radii = 1100 feet, the vertical height of the tower $${\large\frac{{1063}}{{1100}}}$$ radii. Thus, $$\sin(\theta) = {\large\frac{{1063}}{{1100}}}$$ radii. We find the inverse sine of both sides of the equation, yielding $$\theta = \arcsin\left( {\large\frac{{1063}}{{1100}}} \right)$$ radians. With a calculator we find that the angle measure θ is approximately 1.3107 radians, or 75.1 degrees.
Can you solve the problem at the introduction of this chapter using just the sine function?
While visiting Washington DC you notice that your line of sight to the top of the Washington Monument is about 25 degrees. Estimate your walking distance to the monument given that we know its height is 555 feet.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
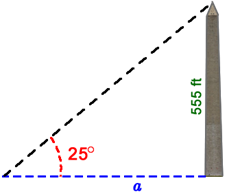 No, we could not solve this problem using only the sine function. The sine of an angle in a right triangle is the ratio of the side opposite the angle to the hypotenuse. The length of the side opposite the 25-degree angle is the height of the Washington Monument or 555 feet. The hypotenuse of the triangle is your distance from the top of the monument. The sine function determines the direct distance to the top of the Washington Monument, but not the walking distance to the monument. We will return to this problem later when we have more tools to help us solve it.
No, we could not solve this problem using only the sine function. The sine of an angle in a right triangle is the ratio of the side opposite the angle to the hypotenuse. The length of the side opposite the 25-degree angle is the height of the Washington Monument or 555 feet. The hypotenuse of the triangle is your distance from the top of the monument. The sine function determines the direct distance to the top of the Washington Monument, but not the walking distance to the monument. We will return to this problem later when we have more tools to help us solve it.
Example 3. Generalizing and Using Sine To Find Quantities
Figure 8-5 shows a right triangle with an angle measure θ radians. Consider the relationship between the angle measure θ radians, the length b of the side opposite this angle, and the length c of the hypotenuse of the triangle, with c and b measured in the same units. In this case, we can always use the hypotenuse as the radius of a circle centered at the vertex of the angle.

Figure 8-5
It is also useful to recall that when working in the unit circle context that $$\sin(\theta) = y$$ , where y the second coordinate of the point where the terminal ray of the angle intersects the circle (Figure 8-6).

Figure 8-6
- Using the sine function, express the relationship between the measurements q, b,and c, as illustrated in Figure 8-5.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
For an input of θ radians, $$\sin(\theta)$$ represents the vertical distance (measured in radii) of the point on the circle above the horizontal diameter. This distance is the ratio of the vertical distance and the radius (as measured in their given units), or $${\large\frac{b}{c}}$$. Thus, we can write $$\sin(\theta) = {\large\frac{b}{c}}$$.
- Using the relationship that $$\sin(\theta) = {\large\frac{b}{c}}$$, as illustrated in Figure 8-5 above, we see that $$\sin(\theta)$$ is equal to the ratio of the side opposite the angle whose measure is θ, and the hypotenuse. Using this relationship, determine the unknown quantities in the right triangles given below.
- Angle measure θ in Figure 8-7
- Length b in Figure 8-8
- Length of the hypotenuse in Figure 8-9
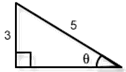
Figure 8-7
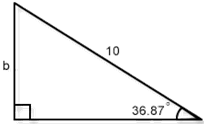
Figure 8-8
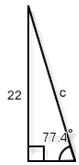
Figure 8-9
Think about it for a moment and then access this link  to view our answer.
to view our answer.
Since sin(θ) = $${\Large\frac{\rm{opposite}}{\rm{hypotenuse}}}$$
- $$\theta= \arcsin\left({{\large\frac{3}{5}}}\right)\approx $$ 0.644 radians;
- $$\sin\left( {\large\frac{{36.87}}{{360}}} \cdot 2\pi \right) = {\large\frac{b}{{10}}}$$, so $$b = 6$$;
- $$\sin\left( {\large\frac{{77.4}}{{360}}} \cdot 2\pi \right) = {\large\frac{22}{{c}}}$$, so $$c = 22.54$$.
Note that the triangles in parts i and ii have the same ratio of the length of the opposite side to the length of the hypotenuse. Also, the angle measurements for the corresponding angles are the same. These triangles are said to be similar. Recall that two triangles are similar if the corresponding (matching) angle measurements are equal or the ratios of their corresponding sides are equal.
Example 4. Co-variation with Sine
Experiment with the Applet 8-1 below to see how changing the angle measure or hypotenuse length will influence the value of $$\sin(\theta)$$.
CLICK  to Open Simulation
to Open Simulation
- In Applet 8-1, as you increase the length of the hypotenuse of the right triangle, describe how the angle measure θ and the length of the side opposite the angle vary.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
All triangles generated are similar to each other. The angle measurement does not change, but the given length of side opposite the angle increases. This length increases such that the ratio $$\sin(\theta)$$ of the length of the opposite side to the length of the hypotenuse remains constant.
- As you increase the openness of the angle θ, describe how the length of the side opposite of the angle and the hypotenuse of the triangle vary.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
As the angle measurement increases, the length of the hypotenuse remains constant, but the length of the side opposite the angle increases.
- As you increase the openness of the angle θ, describe how the ratio $$\sin(\theta)$$ of the length of the opposite side to the length of the hypotenuse varies.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
As the angle measurement increases, the length of the hypotenuse remains constant, but the length of the side opposite the angle increases. Thus, the ratio $$\sin(\theta)$$ of the length of the opposite side to the length of the hypotenuse increases from 0 to 1 as the angle measure increases from 0 to $$\pi$$ radians (0 to 90 degrees).
2. Triangle Trigonometry and Cosine
Let's return to the Eiffel Tower situation.
Example 5. The Eiffel Tower and Determining Angles Using Cosine
Determine the measure of the angle formed by the beam-line that the ranger makes with the top of the tower and the line of sight of the tourist to the base of the tower. As the tourist on the ground peers at the Eiffel Tower with his range finder, he determines that he is 2000 feet away from the base of the tower and that the length of the beam from the range finder, to the top of the tower, is 2265 feet. As before, we would like to know the measure of the angle formed by the beam-line that the ranger makes with the top of the tower and the line of sight of the tourist to the base of the tower (Figure 8-10).

Figure 8-10
Solution
You may have noticed that in Figure 8-10, the orientation of the right triangle has changed, that the angle is opening to the left. As before, we can determine the proportion (or percentage) of arc length cut off by the angle by using the hypotenuse as the radius of a circle centered at the vertex of the angle of measure θ.
In order to orient the right triangle such that the angle opens from the 3 o’clock position, we can rotate or flip the right triangle, while maintaining the side lengths and angle measures (Figure 8-11).

Figure 8-11
Next, knowing that the length of the radius, also known as the hypotenuse of the right triangle, is 2265 feet and the horizontal distance is 2000 feet, determine the horizontal distance in radii.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
The radius of the circle is 2265 feet. Thus, the horizontal distance is $${\large\frac{{2000}}{{2265}}}$$ radii (approximately 0.883 radii).
Recall from Module 7 that $$\cos(\theta)$$ also represents this horizontal distance in radii. Using this, we can write $$\cos(\theta) ={\large\frac{{2000}}{{2265}}}$$. Thus, our goal is to find the angle measure, or the input θ to cosine, such that the output value, $$\cos(\theta)$$, is equal to $${\large\frac{{2000}}{{2265}}}$$.
Recall that arccosine is defined to be the inverse of cosine restricted to the interval $$[0,\;\pi]$$ and we are interested in a value of q in this interval so that $$\arccos (\cos (\theta )) = \theta $$. Thus we can determine qby finding the arccosine of the expressions on both sides of the equal sign.
\[\theta =\arccos\left({\large\frac{{2000}}{{2265}}}\right)\]
Using a calculator we find that $$\arccos\left({\large\frac{{2000}}{{2265}}}\right)\approx 0.4886$$ radians, resulting in an angle measure $$\theta\approx 0.4886$$ radians. We say that the angle has a measure θ of approximately 0.4886 radians or 27.99 degrees.
- Determine the angle of the line of sight for a tourist who is standing on the ground 1100 feet from the top of the tower and 282.9 feet from the base of the tower?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
Using the same method as above, the 1100-foot hypotenuse becomes the radius of the constructed circle (Figure 8-10). Using this, we determine that the horizontal distance is $${\large\frac{{282.9}}{{1100}}}$$ radii. Thus, we need to determine the input θ radians such that $$\cos(\theta) ={\large \frac{{282.9}}{{1100}}}$$. We find the inverse cosine of both sides of the equation, yielding $$\theta = \arccos\left({\large\frac{{282.9}}{{1100}}}\right)$$. With a calculator we find that the angle measure θ is approximately 1.3107 radians, or 75.1 degrees.

Figure 8-12
Example 6. Generalizing and Using Cosine To Find Quantities
For any right triangle with an angle measure θ radians as shown in Figure 8-13, consider the relationship between θ radians, the length a of the side adjacent this angle, and the length c of the hypotenuse of the triangle, with c and a measured in the same unit. In this case, we use the hypotenuse as the radius of a circle centered at the vertex of the angle.
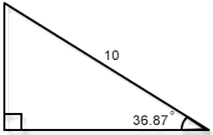
Figure 8-13
- Using the cosine function, express the relationship between the measurements q, a,and c.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
For an input of θ radians, $$\cos(\theta)$$ represents the horizontal distance, in radii, of the point on the circle to the right of the vertical diameter. This distance is the ratio of the horizontal distance and the radius (as measured in their given units), or $${\large\frac{{a}}{{c}}}$$. Thus, we can write $$\cos(\theta) ={\large\frac{{a}}{{c}}}$$.
- Given the right triangles below, find the value of the following quantities:
- Angle measure θ in Figure 8-14
- Length $$a$$ of the adjacent side in Figure 8-15
- Length c of the hypotenuse in Figure 8-16
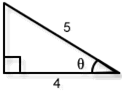
Figure 8-14

Figure 8-15

Figure 8-16
Think about it for a moment and then access this link  to view our answer.
to view our answer.
Using the relationship, determined above, between the side adjacent the marked angle and the hypotenuse, we have:
- $$\theta = \arccos\left({{\large\frac{4}{5}}}\right)\approx 0.644$$ radians
- $$cos \left( {\large\frac{{36.87}}{{360}}} \cdot 2\pi \right) = {\large\frac{a}{{10}}}$$, so $$a = 8$$
- $$\cos\left( {{\large\frac{{77.4}}{{360}}} \cdot 2\pi } \right) = {\large\frac{4.92}{{c}}}$$, so $$c = 22.55$$
Note that the triangles in parts i and ii have the same ratio of the length of the adjacent side to the length of the hypotenuse. Also, the angle measurements for the corresponding angles are the same. These triangles are said to be similar.
Example 7. Co-variation with Cosine
Experiment with the Applet 8-2 below to see how changing the angle measure or hypotenuse length will influence the value of $$\cos(\theta)$$.
CLICK  to Open Simulation
to Open Simulation
- In Applet 8-2, as you increase the length of the hypotenuse of the right triangle, describe how the angle measure θ and the length of the side adjacent to this angle vary.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
All triangles generated are similar to each other. The angle measurement does not change, but the given length of the side adjacent to the angle decreases. This length decreases such that the ratio $$\cos(θ)$$ of the length of the adjacent side to the length of the hypotenuse remains constant.
- As you increase the openness of the angle θ, describe how the length of the side adjacent to the angle and the hypotenuse of the triangle vary.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
As the angle measurement increases, the length of the hypotenuse remains constant, but the length of the side adjacent to the angle decreases.
- As the angle measure θ increases from 0 to 90 degrees but the length of the hypotenuse remains constant, describe how $$\cos(\theta)$$ varies.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
As the angle measure θ increases from 0 to 90 degrees, the length of the side adjacent to the angle decreases from the length of the hypotenuse to 0. Thus, the ratio $$\cos(\theta)$$ of the length of the adjacent side and the hypotenuse decrease from 1 to 0, as the angle measure θ increases from 0 to 90 degrees.
Example 8. The Boat Problem
A boat leaves a dock traveling at 31 degrees north of east (see Figure 8-13) traveling at a 18.5 nautical miles per hour (a nautical mile per hour is a unit of measurement of nautical speed equivalent to 1.151 miles per hour). At some point along the journey the boat’s beacon malfunctions, leaving it impossible for its docking station to track the boat’s location. . Given this information, we would like to track how far east and how far north the boat has traveled at any given time.
We represent the problem using a right triangle. The path of the boat forms the hypotenuse of the right triangle, with the distance traveled by the boat to the east (length of adjacent side) and the distance traveled by the boat to the north (length of opposite side) used as the lengths of the legs of the triangle.
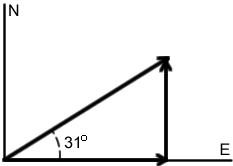
Figure 8-17
Experiment with the Applet 8-3 below to see how the motion of the boat influences the length of the sides of the right triangle formed by the path of the boat and the corresponding east and north distances traveled.
CLICK  to Open Simulation
to Open Simulation
We note that the distance traveled by the boat (length of the hypotenuse) increases as the time elapsed since the boat left the dock increases, and thus the distances traveled east and north will increase with respect to increases in the elapsed time. The distance traveled by the boat measured in nautical miles d increases at a rate of 18.5 nautical miles per hour.
- If we choose t to measure the elapsed time in hours, what is the formula that relates the distance traveled (in nautical miles) by the boat to the elapsed time?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
The formula is $$d = 18.5t$$ since the number of nautical miles traveled is 18.5 times as large as the number of hours traveled.
An illustration of these relationships is given in Figure 8-18.
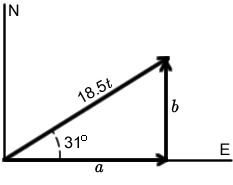
Figure 8-18
Now that we have the hypotenuse and an angle measure of the right triangle, we can use trigonometric functions to relate these quantities to the varying north and east distances traveled.
First, notice that the distance traveled north measured in nautical miles b is the length of the side opposite the 31 degree angle. Thus, we can use the sine function to determine the number of nautical miles traveled north. Recall that we need to first convert the angle measure to radians.
- How many radians is 31 degrees?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
31 degrees corresponds to cutting off an arc length that is $${\large\frac{{31}}{{360}}}$$ of the circumference of a circle centered at the vertex of the angle. Thus, the angle cuts off the same proportion of $$2\pi$$ resulting in an angle measurement of $${\large\frac{{31}}{{360}}}$$ $$(2\pi)$$, or approximately 0.541 radians.
We now have the relationship of $$\sin\left( {{\large\frac{{31}}{{360}}} \cdot 2\pi } \right) = {\large\frac{b}{{18.5t}}}$$. Thus, the distance traveled north as a function of time since leaving the dock is $$b = f(t) = 18.5\sin\left( {{\large\frac{{31}}{{360}}} \cdot 2\pi } \right)t$$, or approximately $$b = f(t) = 9.527t$$, where $$t$$ is measured in hours and $$b$$ is measured in nautical miles.
- Create a cosine function to model the number of nautical miles traveled east a as a function of the number of hours t traveled.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
We have the relationship of $$\cos\left( {{\large\frac{{31}}{{360}}} \cdot 2\pi } \right) ={\large \frac{a}{{18.5t}}}$$. Thus, the distance traveled east as a function of time since leaving the dock is $$a = g(t) = 18.5\cos\left( {\frac{{31}}{{360}} \cdot 2\pi } \right)t$$, or approximately $$a = g(t) = 15.858t$$, where $$t$$ is measured in hours and $$a$$ is measured in nautical miles.
In this section we examined the sine and cosine functions in the context of a right triangle. These investigations led us to describe how the sine and cosine functions map an angle measure to the ratio of two sides of a right triangle (Figure 8-19).
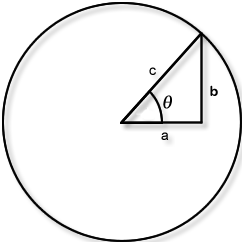
Figure 8-19
Figure 8-19 illustrates $$\sin(\theta) ={\large \frac{{b}}{{c}}}$$ and $$\cos(\theta) ={\large \frac{{a}}{{c}}}$$ , where b represents the length of the leg opposite the angle of measure θ, a represents the length of the leg adjacent to the angle of measure θ, and c represents the length of the hypotenuse (See Figure 8-19).
3. The Tangent Function
This section introduces another trigonometric function, the tangent function. This function is defined in terms of the sine and cosine functions.
Given an angle measure θ, the tangent of θ is the ratio of the sin (θ) to $$\cos(\theta)$$, also written,
\[\tan(\theta)={\large\frac{\sin(\theta)}{\cos(\theta)}}\]
We note that the tangent function is not defined for values of θ for which$$\cos(\theta)=0$$.
We’ll explore the tangent function in more detail in the examples that follow.
Example 9. The Ratio of the Sine Function to the Cosine Function
- Given these relationships, what is the ratio of $$\sin(\theta)$$ to $$\cos(\theta)$$? That is, what is $${\large\frac{{\sin \left( \theta \right)}}{{\cos \left( \theta \right)}}} $$?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
\[\frac{\sin(\theta)}{\cos(\theta)}={\Large\frac{\left(\frac{b}{c}\right)}{\left(\frac{a}{c}\right)}}\rm{\;which\;yields\;}\frac{\sin(\theta)}{\cos(\theta)}=\frac{b}{c}\]
Recall that $$\sin(\theta)$$ represents the length of the opposite side measured in radii and $$\cos(\theta)$$ represents the length of the adjacent side measured in radii. Thus, the ratio $${\large\frac{{\sin \left( \theta \right)}}{{\cos \left( \theta \right)}}} $$ is equivalent to the ratio $${\large\frac{{b}}{{a}}} $$.
- Given this relationship, if the angle measure θ in Figure 8-19 remains constant, while the length of the side adjacent to the angle of measure θ increases, how does the length of the side opposite the angle of measure θ vary?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
As the length of the adjacent side increases, the length of the side opposite this angle must also increase so that the ratio $${\large\frac{{b}}{{a}}}$$ remains constant. Thus, if the length of the adjacent side is increased by a factor of 1.5, the length of the side opposite this angle must also increase by a factor of 1.5.
The trigonometric function named tangent defines the relationship between an angle with a measure of θ and the lengths of the sides opposite and adjacent to the angle of measure θ . That is $$\tan(\theta) = {\large\frac{{\sin \left( \theta \right)}}{{\cos \left( \theta \right)}}} $$, or $$\tan(\theta) ={\large\frac{{b}}{{a}}} $$.
- Given the right triangles below, use the tangent and inverse tangent functions to find the value of the following quantities:
- Angle measure θ in Figure 8-20
- Length a of the adjacent side in Figure 8-21
- Length of the hypotenuse in Figure 8-22
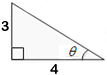
Figure 8-20

Figure 8-21

Figure 8-22
Think about it for a moment and then access this link  to view our answer.
to view our answer.
- $$\theta= \tan^{ - 1}\left( {{\large\frac{3}{4}}} \right)\approx 0.644$$ radians or 36.87 degrees
- $$\tan\left( {\large\frac{77.4}{360}} \cdot 2\pi \right) = {\large\frac{6}{a}}$$, so $$a = 8$$
- $$\tan\left( {\large{\frac{36.87}{{360}}}} \cdot 2\pi \right) = {\large\frac{b}{{4.92}}}$$, so $$b = 22$$
The triangles in i and ii are similar: the ratios of the side opposite the designated angle to the side adjacent to the designated angle are equal. Also, the angle measurements for the corresponding angles are equal.
Experiment with the Applet 8-4 below to see how changing the angle measure or hypotenuse length influences the value of $$\tan(\theta)$$.
CLICK  to Open Simulation
to Open Simulation
- In Applet 8-4, as you increase the length of the hypotenuse of the right triangle, describe how the angle measure θ and the lengths of the opposite and adjacent sides to the angle vary.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
All triangles generated are similar to each other. The given angle measurement does not change, but the lengths of the sides opposite and adjacent to the angle increase. However, these lengths increase such that they remain in a constant ratio. That is, the ratio $$\tan(\theta)$$ of the length of the opposite side to the length of the adjacent side remains constant.
- As you increase the openness of the angle θ , describe how the lengths of the sides of the right triangle vary.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
As the angle measurement increases, the length of the hypotenuse remains constant, but the length of the opposite side increases while the length of the adjacent side decreases.
- As you increase the openness of the angle θ , describe how the ratio $$\tan(\theta)$$ of the length of the opposite side to the length of the adjacent side varies.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
As the angle measurement θ increases, the length of the hypotenuse remains constant, but the length of the opposite side increases while the length of the adjacent side decreases. The ratio $$\tan(\theta)$$ of the length of the opposite side to the length of the adjacent side increases without bound from 0, as θ increases from 0 to $$\pi$$ radians (0 to 90 degrees).
Summary of Trigonometric Functions and Right Triangles
Given any right triangle with an angle measure of θ and side lengths of $$a$$, $$b$$, and $$c$$, we can orient the right triangle such that the angle opens from the 3 o’clock position of a circle formed by the hypotenuse of the right triangle (Figure 8-23).
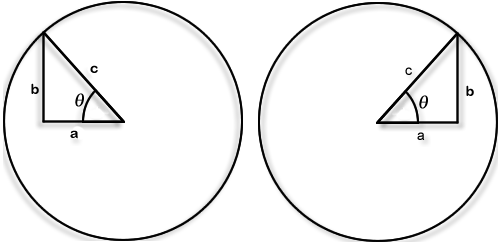
Figure 8-23
In such a case, we can write the following relationships between the sides of the right triangle and the angle measure radians.
\[\sin(\theta) = \frac {{b}}{{c}}\quad\quad\quad\cos(\theta) = \frac {{a}}{{c}}\quad\quad\quad\tan(\theta) = \frac {{b}}{{a}}\]
4. Tangent and the Unit Circle
Recall that in Module 7 we investigated the trigonometric functions of sine and cosine relative to the unit circle. Let’s now explore the meaning of the tangent function in terms of the unit circle (Figure 8-24).
First, we construct a right triangle inside a unit circle. The vertex of one of its acute angles lies at the origin and its hypotenuse becomes a radius of the unit circle, as illustrated in Figure 8-24. Thus, if a point on the unit circle has coordinates $$(x,\; y)$$, then $$\tan(\theta) = {\large\frac {{y}}{{x}}}$$ since the y-value represents the length of the side opposite θ and the x-value represents the length of the side adjacent to θ.
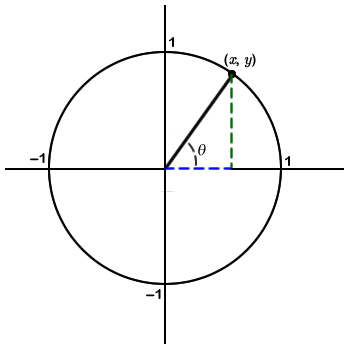
Figure 8-24
Example 10. Exploring the Tangent Function
Suppose an angle measuring θ radians cuts an arc on the unit circle that starts at the point (1, 0) and extends counterclockwise to the point $$(x,\; y)$$, as shown in Figure 8-25. As θ varies so does the ratio, $$\tan(\theta)={\large\frac{y}{x}}$$.
For instance, $$\tan\left({\large\frac {{\pi}}{{4}} }\right )= 1$$ means that the ratio $${\large\frac {{y}}{{x}}}$$ of the vertical displacement to the horizontal displacemnent is 1 when the radius opens $${\large\frac {{\pi}}{{4}}}$$ radians counter-clockwise from the 3 o’clock position. That is, when $$\theta = {\large\frac {{\pi}}{{4}}}$$ radians, the vertical displacement and horizontal displacement are equal.
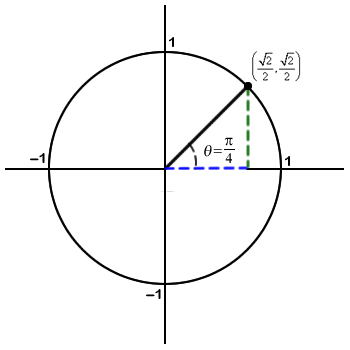
Figure 8-25
- How does the value of $$\tan(\theta)$$ vary as θ increases from 0 to $${\large\frac {{\pi}}{{2}}}$$ radians?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
As θ varies from 0 to $${\large\frac {{\pi}}{{2}}}$$ radians, the vertical distance of the point from the center of the circle increases from 0 to 1 and the horizontal distance of the point from the center of the circle decreases from 1 to 0. Thus, the ratio $$\tan(\theta)$$ of the vertical distance to the horizontal distance of the point from the center of the circle, increases without bound from 0 to $${\large\frac{\pi}{2}}$$.
- Is $$\tan\left({\large \frac {{\pi}}{{2}}} \right )$$ defined?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
No, at an angle measure of $${\large\frac {{\pi}}{{2}}}$$ radians counter-clockwise from the 3 o’clock position, the horizontal distance of the point from the center of the circle is 0, resulting in a division by zero in the ratio $${\large\frac {{y}}{{x}}}$$. Thus the ratio of the vertical distance to the horizontal distance from the center of the circle is not defined when $$\theta={\large\frac{\pi}{3}}$$.
- How does the value of tan(\theta) vary as θ decreases from 0 to $$-{\large \frac {{\pi}}{{2}}}$$ radians?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
As θ varies from 0 to $$- {\large\frac {{\pi}}{{2}}}$$ radians, the vertical displacement of the point from the center of the circle decreases from 0 to –1 and the horizontal displacement of the point from the center of the circle decreases from 1 to 0. Thus, the ratio $$\tan(\theta)$$ of the vertical displacement to the horizontal displacement of the point from the center of the circle, decreases without bound from 0.
- How does the value of $$\tan(\theta)$$ vary as θ decreases from $${\large\frac {{\pi}}{{2}}}$$ to $$\pi$$ radians?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
As θ varies from $${\large\frac {{\pi}}{{2}}}$$ to $$\pi$$ radians, the vertical displacement of the point from the center of the circle decreases from 1 to 0 as the horizontal displacement of the point from the center of the circle decreases from 0 to –1. Thus, the ratio $$\tan(\theta)$$ of the vertical displacement to the horizontal displacement of the point from the center of the circle is 0 when $$\theta = \pi$$, and decreases without bound as $$\theta \to {{\large\frac{\pi }{2}}^ + }$$.
- Determine the graph of y = f(\theta) = tan(\theta) as θ varies from $$- {\large\frac {{\pi}}{{2}}}$$ to $${\large\frac {{\pi}}{{2}}}$$ radians?
Think about it for a moment and then access this link  to view our answer.
to view our answer.

Figure 8-26
- What are the vertical asymptotes of the graph in Figure 8-26 above?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
The vertical asymptotes occur at $$\theta = -{\large \frac {{\pi}}{{2}}}$$ and $$\theta = {\large\frac {{\pi}}{{2}}}$$. Using limit notation, we have $$\mathop {\lim }\limits_{\theta \to - {{{\large\frac{\pi }{2}}}^ + }} \tan(\theta) = –\infty$$ and $$\mathop {\lim }\limits_{\theta \to - {{{\large\frac{\pi }{2}}}^ - }} \tan(\theta) = \infty$$ .
Example 11. Exploration of Tangent
Given the graph of $$y = f(\theta) = \tan(\theta)$$ as θ varies from $$– 4\pi$$ to $$4\pi$$ radians.
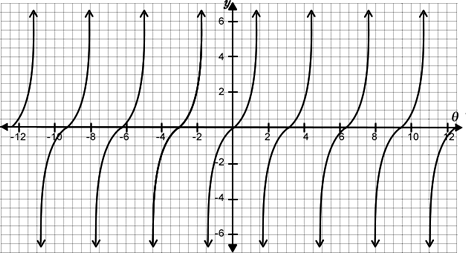
Figure 8-27
- When the value of θ is $$- {\large\frac {{7\pi}}{{2}}}$$, $$- {\large\frac {{5\pi}}{{2}}}$$, $$- {\large\frac {{3\pi}}{{2}}}$$, $$- {\large\frac {{\pi}}{{2}}}$$, $${\large\frac {{\pi}}{{2}}}$$, $$ {\large\frac {{3\pi}}{{2}}}$$, $${\large \frac {{5\pi}}{{2}}}$$, and $$ {\large\frac {{7\pi}}{{2}}}$$, the value of tan(θ) is undefined. Why is this so?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
At those values of θ , the horizontal distance of the point from the center of the circle is 0, thus the ratio $$tan(\theta)$$ of the vertical distance of the point to the horizontal distance of the point from the center of the circle is undefined.
- What is the period of the tangent function?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
Since the output values of the tangent function repeat the same pattern as q varies over an interval of π radians, the period of the tangent function is π radians.
We notice that the tangent function is periodic and has vertical asymptotes at the beginning and end of each period of the tangent function, -3π/2, -π/2, π/2, 3π/2, 5π/2, etc.
Example 12. The Gateway Arch
While eating lunch in downtown St. Louis, you noticed a sign indicating that the Gateway Arch is exactly 0.1 mile from the restaurant where you were eating. While eating lunch you attempted to guess the height of the Gateway Arch using your calculator. What quantities could you use to estimate the height of the Gateway Arch?
One option is to estimate the angle at which you have to look up to view the top of the arch (Figure 8-28), and use this estimation and a trigonometric function to determine the approximate height of the Gateway Arch.

Figure 8-28
Notice that the line of sight to the top of the arch, a vertical line from the ground to the peak of the arch, and the 0.1 mile length form a right triangle. After estimating that the angle at which you looked up to see the peak of the arch is 50 degrees, use this estimation to approximate the height of the Gateway Arch?
Think about it for a moment and then access this link  to view our answer.
to view our answer.
The length of the side adjacent to the 50-degree angle is 0.1 mile. Since the vertical line reaching to the peak of the arch is the side opposite the angle, the tangent function can be used to determine the length of this unknown side (i.e., the height of the arch). We convert degrees to radians by dividing 50 by 360; then multiplying by $$2\pi$$ and write $$\tan\left( {\large{\frac{50}{{360}}} \cdot 2\pi } \right) = {\large\frac{h}{{0.10}}}$$. We conclude that the height of the Gateway Arch is approximately 0.12 miles (634 feet).
Let’s now return to the question that was posed in the introduction of this module.
Example 13. The Washington Monument
Given that the Washington Monument is 555 feet high and the approximate angle of a tourist’s line of sight to the top of the monument is 25 degrees. Determine a function that relates θ (in degrees) with the distance from the tourist to the base of the Washington Monument.
Think about it for a moment and then access this link  to view our answer.
to view our answer.
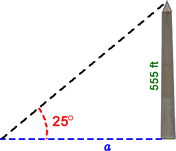
Figure 8-29
We draw Figure 8-29, emphasizing the right triangle in the problem situation. We observe that $$\tan\left( {{\large\frac{25}{{360}}} \cdot 2\pi } \right) = {\large\frac{555}{{a}}}$$. Therefore, for this tourist, the walking distance to the Washington Monument is given by $$a = {\large\frac{{555}}{{\tan \left( {{\large\frac{{25}}{{360}}} \cdot 2\pi } \right)}}} = 1190$$. The tourist is 1190 feet from the base of the Washington Monument. In general, the walking distance a (measured in feet) to the Washington Monument can be written as a function of the angle θ (measured in degrees) of the line of sight to the top of the Monument:
\[a = f(\theta) = \frac{{555}}{{\tan \left( {\frac{{25}}{{360}} \cdot 2\pi } \right)}}\]
5. Trigonometric Identities
Consider the unit circle in Figure 8-30. For any point $$(x,\; y)$$ on the unit circle, we can use the Pythagorean Theorem to verify that $$x^2+y^2=1$$. Also, for any point $$(x,\;y)$$ on the unit circle, we previously established that,
\[x = cos(\theta)$$ and $$y = \sin(\theta)\]
Since $$x^2+y^2=1$$, we can substitute the expressions $$\cos(\theta)$$ and $$\sin(\theta)$$ for $$x$$ and $$y$$ respectively to obtain the identity called the Pythagorean identity, which is $$(\cos(\theta))^2 + (\sin(\theta))^2 = 1$$.

Figure 8-30
The relationship $$(\cos(\theta))^2 + (\sin(\theta))^2 = 1$$ is called an identity because it is true for any value of θ. It is sometimes written as $$\cos^2(\theta) + \sin^2(\theta) = 1$$. The identity $$\cos^2(\theta) + \sin^2(\theta) = 1$$ is one of many useful trigonometric identities.
Trigonometric identities can be used to determine other trigonometric identities. For instance, the Pythagorean identity states that for any input value θ, $$\cos^2(\theta) + \sin^2(\theta) = 1$$. From this identity, we can also state the identities of $$\cos^2(\theta) = 1 – \sin^2(\theta)$$ and $$\sin^2(\theta) = 1 – \cos^2(\theta)$$. In addition, we can multiply both expressions of the Pythagorean identity by $${\large\frac{1}{{{{\cos }^2}(\theta )}}}$$ to obtain $$1 + {\large\frac{{{{\sin }^2}(\theta )}}{{{{\cos }^2}(\theta )}}}= {\large\frac{1}{{{{\cos }^2}(\theta )}}}$$, which cab also written as $$1 + \tan^2 (\theta) ={\large \frac{1}{{{{\cos }^2}(\theta )}}}$$.
Other common trigonometric identities are:

Example 14. Algebraically Proving an Identity
Consider the trigonometric identity of $${\large\frac{{{{\cos }^2}(\theta )}}
{{1 - \sin (\theta )}}} = 1 + \sin(\theta)$$.
To prove a trigonometric identity, we need to transform one expression so that it becomes identical to the other expression. For the identity above, we transform the expression on the left-hand side, using the Pythagorean identity and factoring. Beginning with the expression on the left-hand side of the equality and that $$\cos^2(\theta) = 1 – \sin^2(\theta)$$, we have:
\[\eqalign{{\frac{{{{\cos }^2}(\theta )}}{{1 - \sin (\theta )}}}&= 1 + \sin(\theta)\\ {\frac{{{{1 - \sin }^2}(\theta )}}{{1 - \sin (\theta )}}} &= 1 + \sin(\theta)\\ {\frac{{(1 - \sin (\theta ))(1 + \sin (\theta ))}}{{1 - \sin (\theta )}}} &= 1 + \sin(\theta)\\ 1 + \sin(\theta) &= 1 + \sin(\theta)}\]
Thus, through the use of the Pythagorean identity, we have algebraically proven the trigonometric identity of $${\large\frac{{{{\cos }^2}(\theta )}}{{1 - \sin (\theta )}}} = 1 + \sin(\theta)$$.
Example 15. Geometrically Proving an Identity
Trigonometric identities can also be proven geometrically. Consider the identity of: $$\sin(x + y) = \sin(x)\cos(y) + \cos(x)\sin(y)$$.
Consider the following image of the unit circle with angles of measure $$x$$, $$y$$, and $$x + y$$.
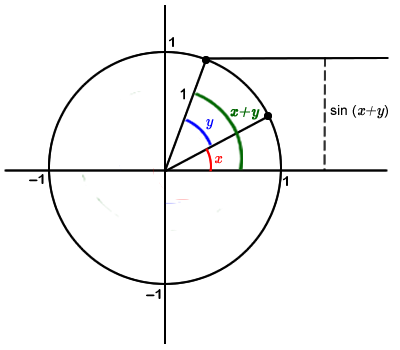
Figure 8-31
We begin by creating a right triangle by constructing a segment perpendicular to the terminal ray of the angle of measure x from the point of intersection of the unit circle and the terminal ray of the angle of measure $$x + y$$ (Figure 8-32).
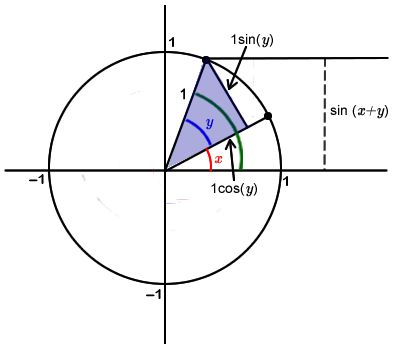
Figure 8-32
In the blue triangle, the side opposite the angle of measure $$y$$ has a length of $$1\cdot\sin(y)$$, and the side adjacent to the same angle has a length of $$1\cdot\cos(y)$$.
Next, construct two more right triangles (highlighted in red in Figure 8-33) by inserting a segment the length of that is perpendicular to the horizontal diameter and passes through the vertex of the right angle of the triangle which we previously highlighted in blue.

Figure 8-33
Notice that the hypotenuse of the bottom triangle has a length $$\cos(y)$$ and the hypotenuse of the top triangle has a length $$\sin(y)$$. If the length of the side opposite of the angle of measure $$x$$ is $$a$$, then $$\sin(x) = {\large\frac{a}{{\cos (y)}}}$$. That is, the length of the side opposite the angle of measure $$x$$ is $$\cos(y)\sin(x)$$ . Thus, we have found the length of one of the segments (see Figure 8-34).

Figure 8-34
To determine the length of the other segment, note that the angle measures in the top triangle are the same as the angle measures in the bottom triangle (see Figure 8-35). We use this, along with angle measure $$x$$, to determine that the side adjacent to angle measure $$x$$ has a length of $$\sin(y)cos(x)$$.

Figure 8-35
With the length of the two segments found, and the known segment length of , we can write the identity $$\sin(x + y) = \sin(x)\cos(y) + \cos(x)\sin(y)$$.
Example 16. Solving Equations Algebraically Using Identities
Suppose we know that $$\sin(\theta) = \sin(2\theta)$$, and are interested in all values of θ satisfying this equation such that $$0 \leq \theta \leq 2\pi $$. (Note that this equation is not an identity, so it is not true for all values of θ, but it might be true for some.) In order to determine the values of θ that make this equation true, we can use trigonometric identities to get the equation in a different form. For instance, we can use the identity $$\sin(2\theta) = 2\sin(\theta)\cos(\theta)$$ to rewrite the equation:
\[\eqalign{\sin(\theta) &= 2\sin(\theta)\cos(\theta)\\ \sin(\theta) – 2\sin(\theta)\cos(\theta) &= 0\\ \sin(\theta)(1 – 2\cos(\theta)) &= 0}\]
Thus, if we determine the values of θ such that $$\sin(\theta)(1 – 2\cos(\theta) = 0$$, these values will satisfy our original equation. Since a product of two factors $$\sin(\theta)$$ and $$1 – 2\cos(\theta)$$ are equal to 0, we can solve for θ by setting the each factor equal to 0 to obtain values for θ that result in a product of 0.
\[\sin(\theta) = 0 \rm{ \quad or \quad } 1 – 2\cos(\theta) = 0\]
Using the unit circle to solve $$\sin(\theta) = 0$$, we have $$\theta=0$$. Using the graphing calculator and unit circle to solve $$1 – 2\cos(\theta) = 0$$, or $$\cos(\theta) = {\large\frac{1}{2}}$$, we have $$\theta = {\large\frac{\pi}{3}}$$,$${\large\frac{5 \pi}{3}}$$. Thus, the equation $$\sin(\theta) = \sin(2\theta)$$ has five solutions, $$\theta=0$$, $${\large\frac{\pi}{3}}$$, $$\pi$$,$${\large\frac{5 \pi}{3}}$$, and $$2\pi$$.





 No, we could not solve this problem using only the sine function. The sine of an angle in a right triangle is the ratio of the side opposite the angle to the hypotenuse. The length of the side opposite the 25-degree angle is the height of the Washington Monument or 555 feet. The hypotenuse of the triangle is your distance from the top of the monument. The sine function determines the direct distance to the top of the Washington Monument, but not the walking distance to the monument. We will return to this problem later when we have more tools to help us solve it.
No, we could not solve this problem using only the sine function. The sine of an angle in a right triangle is the ratio of the side opposite the angle to the hypotenuse. The length of the side opposite the 25-degree angle is the height of the Washington Monument or 555 feet. The hypotenuse of the triangle is your distance from the top of the monument. The sine function determines the direct distance to the top of the Washington Monument, but not the walking distance to the monument. We will return to this problem later when we have more tools to help us solve it.